Skylar Shi | The Ohio State University

About Me

I will be starting my Ph.D. studies in Statistics at the Ohio State University (OSU) this August. Currently, I am working with Xiaotian Zheng on copula mixture models for marked point processes in time, developing a flexible framework to capture multivariate dependencies in event durations and marks.

I received my M.S. in Statistics at University of Washington (UW) in March 2025. My research at UW with Adrian E. Raftery focused on modeling time series based on Bayesian hierarchical models and Bayesian Model Averaging, applied to global temperature forecast. Additionally, I worked with Abel Rodriguze on a one-dimensional factor analysis model, the Probit Unfolding Model, aimed at estimating individual ideology over time from binary preference data.

My research interest lies primarily in dynamic modeling, with a particular emphasis on developing methodologies for spatio-temporal data that exhibit dependencies across different variables and multiple spatio-temporal scales. I am also interested in creating flexible models that operate with minimal restrictive assumptions, as common assumptions like conditional independence often fail to hold in complex stochastic processes. In terms of application, I am excited by the potential of these methodologies to advance research in diverse fields, including climate science, political and social sciences, genetics and neuroscience.

Research Interests

Dynamic modeling: time series, point processes, dependency modeling
Bayesian statistics: hierarchical models, Bayesian Model Averaging
Latent variable models: factor analysis models
Application: climate science, political and social sciences, genetics, neuroscience

News

[June, 2024] Presented a poster on “Copula Mixture Models for Marked Point Processes in Time” at the ICSA Applied Statistics Symposium. [Poster]
[May, 2024] Presented a poster on “Bayesian Implementation of Rogers-Castro Model Migration Schedules” at the UW CSSS 25th Anniversary Conference. [Poster]

Manuscripts

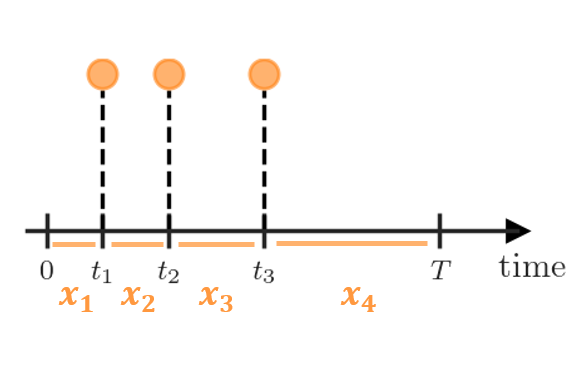Copula Mixture Models for Marked Point Processes in Time

Shi, S. & Zheng, X. (2025+).

Abstract: We propose a copula-based constructive framework for building marked point processes observed over time. In the framework, a marked point process is characterized by the conditional multivariate density of the duration (interval between successive event times) and marks. We model the conditional multivariate density using a finite mixture of transition densities, each incorporating a different lagged duration and its associated marks. These mixture transition densities are constructed by exploiting the decomposition of a high-dimensional densities into bivariate-copula densities and marginal densities. Using bivariate copulas as building blocks allows for flexible modeling of multivariate non-Gaussian dependence among durations and marks. Our approach using copulas, combined with the mixture model formulation for the conditional multivariate density, yields a flexible model for high-order dependence in point processes withmultivariate marks, while retaining computational efficiency. We investigate properties of the point process model analytically and through simulation studies. The methodology is illustrated with an example from the environmental science.

Keywords: Bayesian hierarchical models, conditional mark distribution, Markov chain Monte Carlo, mixture transition distribution models, pair-copula construction.

In preparation

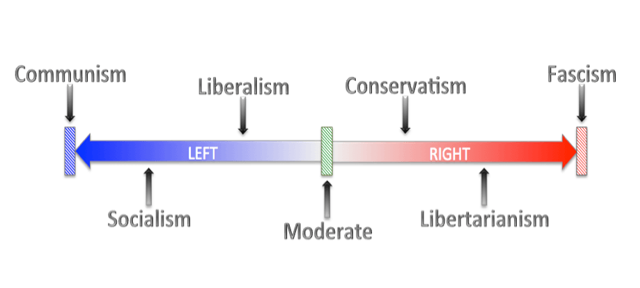pumBayes: Bayesian Estimation of Probit Unfolding Models for Binary Preference Data in R

Shi, S., Rodriguez, A. & Lei, R. (2025+).

Abstract: Probit unfolding models (PUMs) are a novel class of scaling models that allow for items with both monotonic and non-monotonic response functions and have shown great promise in the estimation of preferences from voting data in various deliberative bodies. This paper presents the R package pumBayes, which enables Bayesian inference for both static and dynamic PUMs using Markov chain Monte Carlo algorithms that require minimal or no tunning. In addition to funcitons that carry out the sampling from the posterior distribution of the models, the package also includes various support functions that can be used to pre-process data, select hyperparameters, summarize output, and compute metrics of model fit. We demonstrate the use of the package through an analysis of two datasets, one corresponding to roll-call voting data from the 116th U.S. House of Representatives, and a second one corresponding to voting records in the U.S. Supreme Court between 1937 and 2022.

Keywords: unfolding models, spatial voting models, non-monotonic response function, item response theory, Markov chain Monte Carlo, R, C++.

Submitted to Journal of Statistical Software

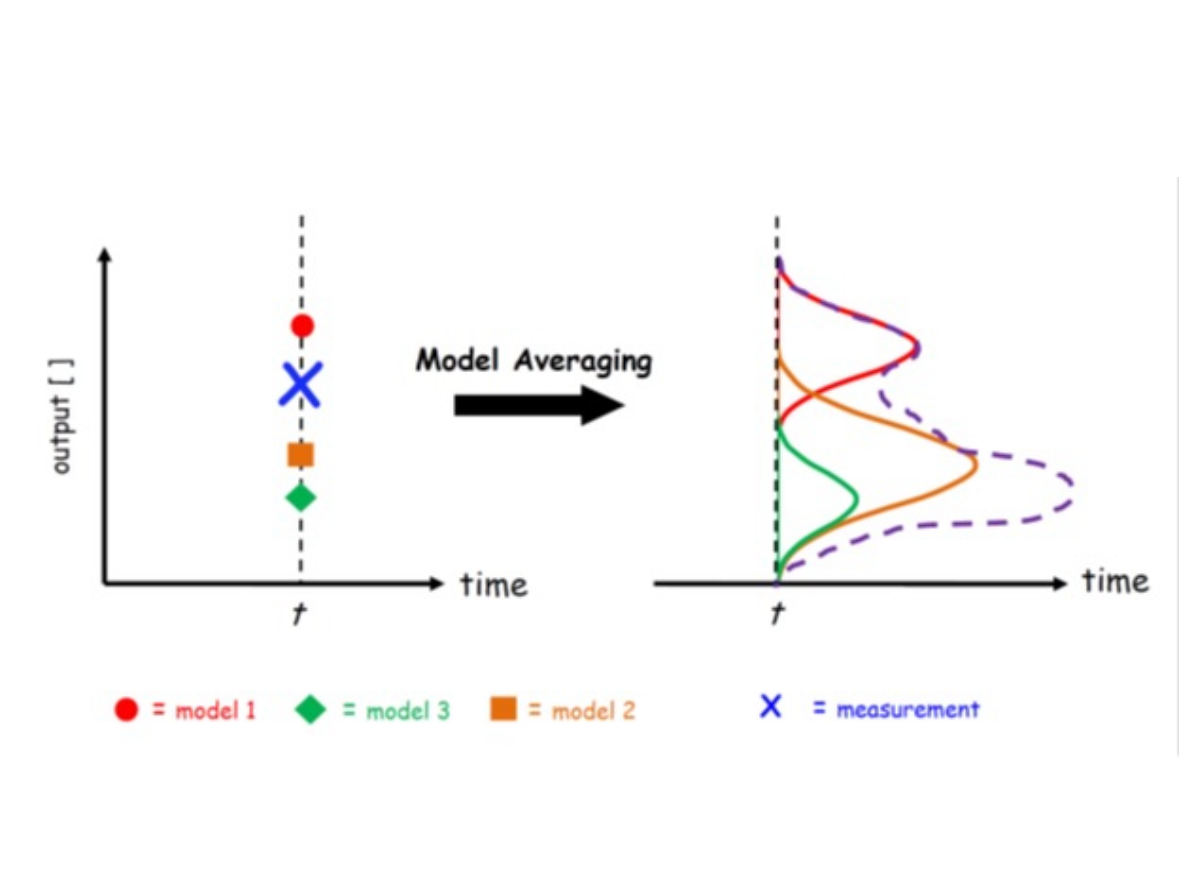Estimating Climate Sensitivity Using Bayesian Model Averaging for CMIP Models

Jiang, J.*, Shi, S.* & Raftery, A. E. (2025+). (*Co-First Authors)

Abstract: In this study, we develop a Bayesian Model Averaging (BMA) framework to improve climate sensitivity estimation by systematically weighting Coupled Model Intercomparison Project (CMIP) models based on their consistency with historical observational data. Unlike traditional approaches that discard models with extreme equilibrium climate sensitivity (ECS) and transient climate response (TCR) values, BMA preserves ensemble diversity while probabilistically downweighting models that deviate from observational trends. We apply BMA to 51 CMIP6 models, deriving a posterior distribution for the transient climate response to cumulative CO₂ emissions (TCRE). Our results show that BMA-based projections systematically yield higher expected warming (36% increase in median TCRE) and lower uncertainty (23% reduction in variance) compared to IPCC AR6 estimates. Variance decomposition analysis reveals that parameter uncertainty in climate sensitivity contributes to 50% of total projection uncertainty, underscoring the need for improved statistical inference in climate modeling. Validation against HadCRUT5 temperature records (2015-2024) demonstrates that the BMA approach is well-calibrated and effectively captures observed temperature trends.

Keywords: Bayesian model averaging, model weighting, climate sensitivity, climate projection, CMIP6.

Submitted to The Annals of Applied Statistics

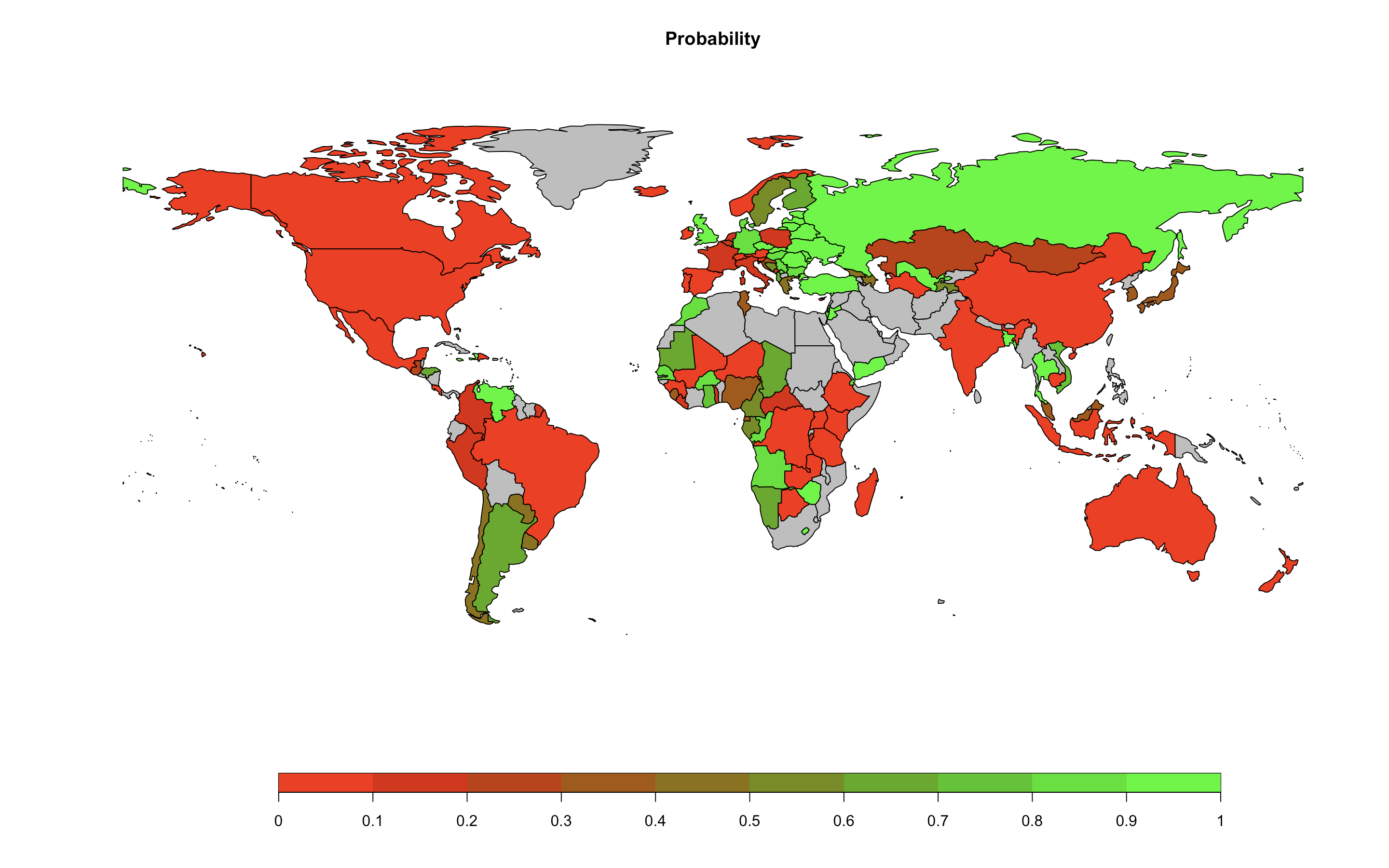Climate Change Implications of Emissions Trends Since the Paris Agreement

Jiang, J.*, Shi, S.* & Raftery, A. E. (2025+). (*Co-First Authors)

Abstract: In this paper, we employed a fully statistical probabilistic model to evaluate the likelihood of achieving the Paris Agreement’s target of limiting global temperature rise to well below 2 °C, with effort to keep it within 1.5 °C. We also conduct country-level assessments based on the nationally determined contributions (NDCs) proposed by each country to help achieve this goal. Based on current trends without additional effort, the median forecast of global mean temperature increase is 2.47 °C, and the probability of staying below 2 °C and 1.5 °C are 15.5% and 1.6%, respectively. However, if all the countries continue to reduce emissions after meeting their NDCs, the probability will increase to 52.4% and 4.6%.

Keywords: Bayesian hierarchical models, global temperature projection, Paris Agreement, nationally determined contributions.

Submitted to Communications Earth and Environment

Publications

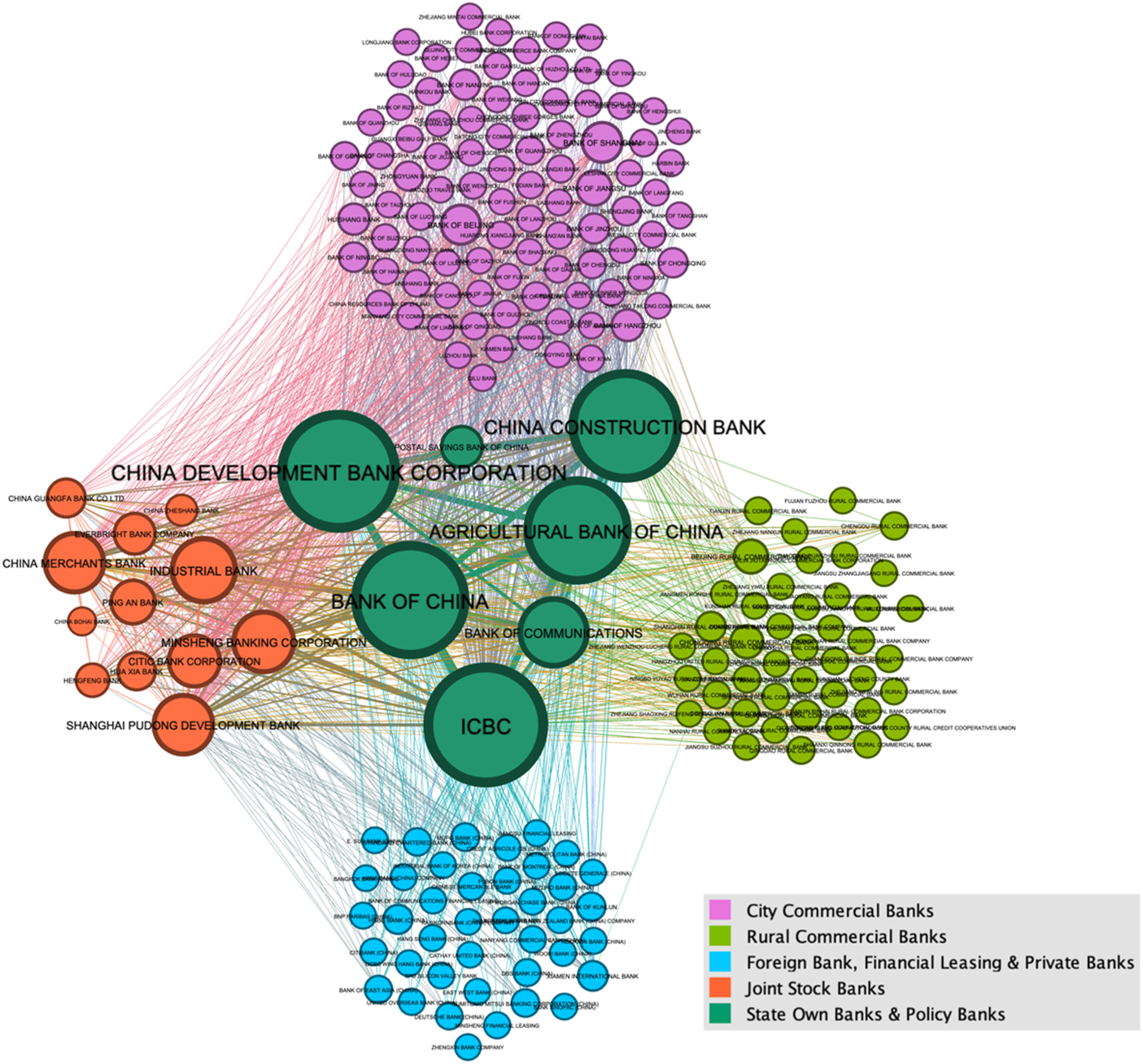Assessing the interconnectedness and systemic risk contagion in the Chinese banking network

Qi, M., Shi, D., Feng, S., Wang, P., & Nnenna, A. B. (2022)

International Journal of Emerging Markets, 17(3), 889-913. 2022.

Abstract: We proposed a network-based approach, grounded in maximum entropy theory, to model systemic risk contagion in the banking sector. We construct a bilateral exposure matrix that estimates interbank exposures by maximizing entropy, which allows for a more realistic approximation of unknown data while preserving known constraints. The network structure was analyzed using network topology theory and centrality measures to assess interconnectedness among banks. Our model simulated risk propagation under both credit and liquidity shocks, examining how these shocks spread across the network. By comparing contagion effects from different shocks situations, we identify how various shock types impact individual bank stability and the overall resilience of the network.

Keywords: risk contagion, interbank market, network topology, credit shock, liquid shock

PDF Code BibTex

Improving oil supply security: using a risk optimization model to China and India

Qi, M., Shi, D., Li, C., Wu, J., & Wang, P. (2021)

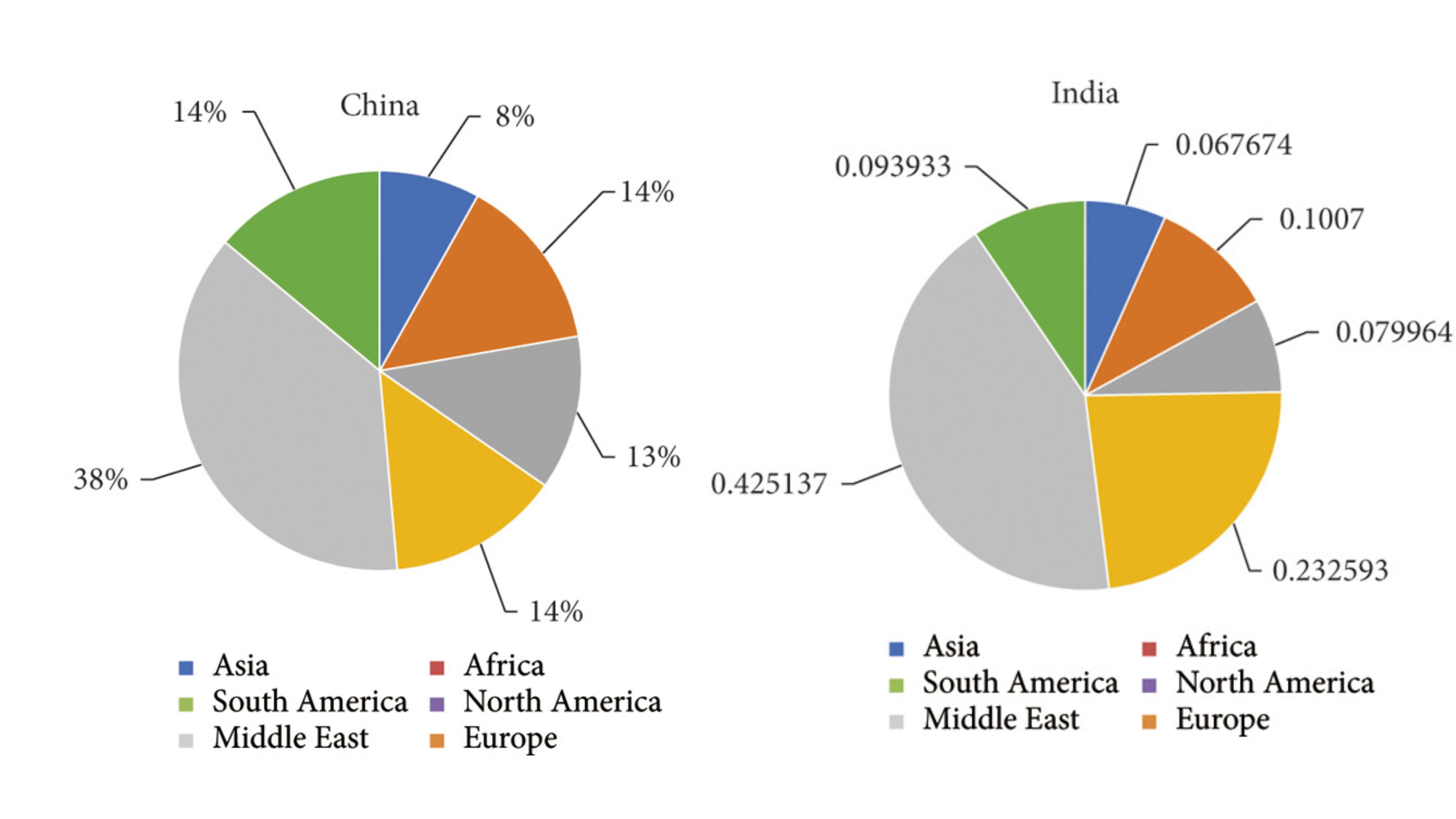Discrete Dynamics in Nature and Society, 2021(1), 5541954.

Abstract: This paper developed a risk optimization model to enhance oil supply security by minimizing risks associated with import sources. The model incorporates key variables including political risk factors of supplier countries, import prices, quantities, and the Herfindahl-Hirschman Index (HHI) to measure diversification, with constraints for domestic consumption and refining capacities. The optimization framework generates an optimal import strategy that reduces dependency on high-risk sources. This methodology provides a strategic tool for managing energy supply risks in volatile geopolitical landscapes. Application results indicated a reallocation of imports for China and India that improves resilience against supply disruptions.

Keywords: risk optimization model, Herfindahl-Hirschman index, supply chain diversification, energy import strategy

PDF BibTex